Parametric Art Systems from Denis Kozlov on Vimeo.
The video spans about a decade of work and much more of research. Below I’ve gathered some links providing additional details, examples and explanations.
More videos:
vimeo.com/211742962 - Procedural Aircraft Design Toolkit
vimeo.com/703402772 - Procedural Creature Generator
The key article covering my vision, process and approach. I’ve
notably advanced in each since the time of writing, but still find it
largely relevant:
the-working-man.org/2018/04/procedural-bestiary-and-next-generation.html
A general overview of the technology involved (at the time of writing
my primary 3D tool being Houdini). No prior knowledge required:
the-working-man.org/2017/04/procedural-content-creation-faq-project.html
The initial 2015 essay noticed by ACM SIGGRAPH:
the-working-man.org/2015/04/on-wings-tails-and-procedural-modeling.html
While the above links mostly focus on 3D part of the work, below is my secret weapon often and easily overlooked: batch image processing (typically with compositing tools like Nuke or Fusion)
The basic principles:
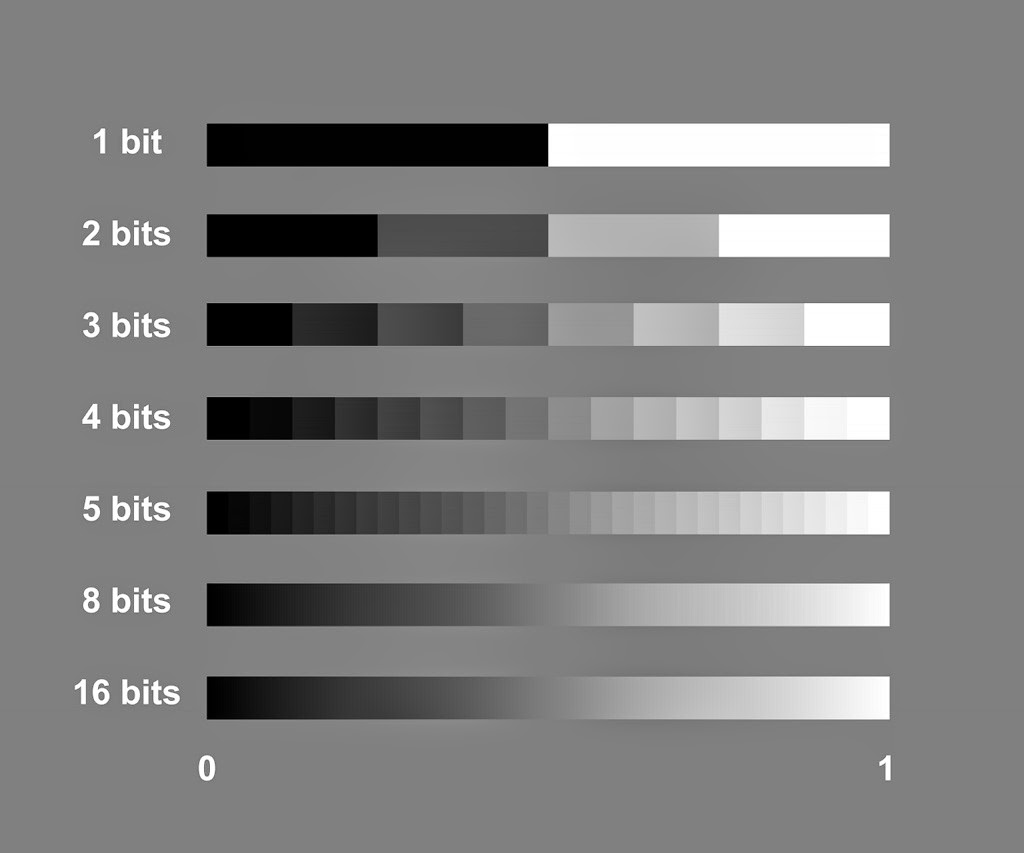
the-working-man.org/2014/11/pixel-is-not-color-square.html
And examples of more advanced techniques:
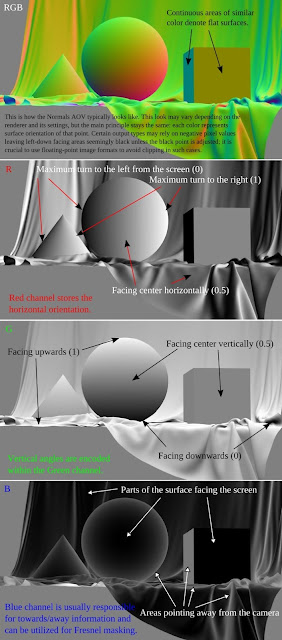
the-working-man.org/2015/08/render-elements-normals.html
the-working-man.org/2015/11/render-elements-uvs.html
Hope you enjoy!